APPLICAZIONI AI TRIANGOLI QUALSIASI
Qui di seguito sono
riportati alcuni esempi di risoluzione
di problemi relativi ai triangoli qualsiasi, utilizzando le formule ricavate
dal teorema dell’altezza (di Montemurro).
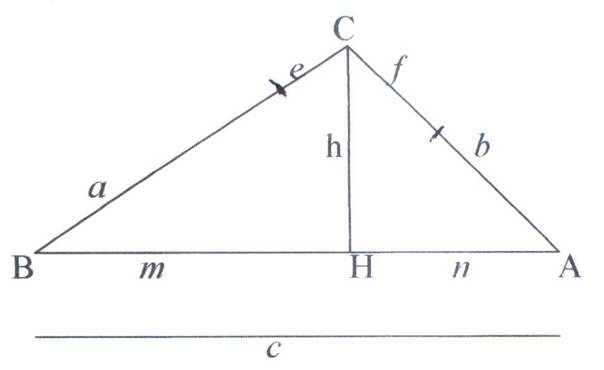
Un triangolo di area 360 cm2 viene diviso dall’altezza in due parti tali
che:
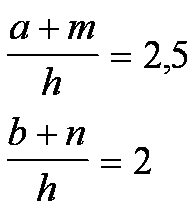
Calcolare le misure dei lati del triangolo.
Si
utilizzano i rapporti dati che
corrispondono rispettivamente ai valori k
e k1 e con la formula inversa dell’area:
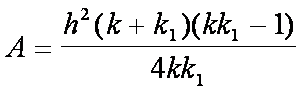
si calcola la misura
dell’altezza che risulta di 20 cm.
Quindi, si ha:
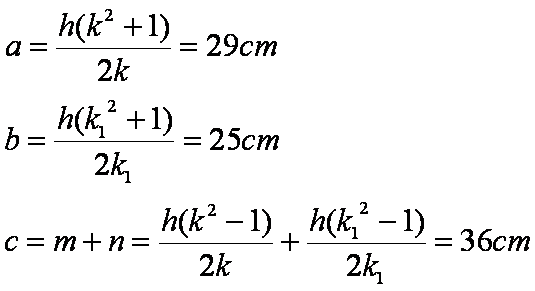
Due triangoli
simili hanno rispettivamente:
2p=216cm; h=18cm;
(il primo) e,
m1=120cm, n1=36cm; (il
secondo).
Determinare il rapporto di similitudine
dei due triangoli.
Nota.
Il rapporto di similitudine dei due triangoli sarà indicato con la lettera R.
Dal
primo triangolo si ottiene:
.
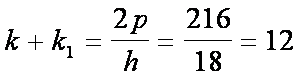Da:
Due triangoli simili hanno rispettivamente:
a+b=50cm; c=40cm (il primo);
a1 =
92.5cm; h1 =30cm (il
secondo).
Determinare
il rapporto di similitudine e calcolare le misure a, b del primo
triangolo.
NOTA. Il rapporto di
similitudine dei due triangoli sarà indicato con la lettera R.
Dal primo dei due triangoli
si ricava il valore kk1
espresso dal rapporto
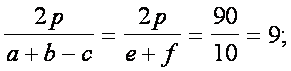
Dal secondo triangolo si
calcola il valore k che è dato dal
rapporto:
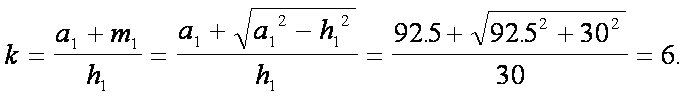
Poiché i due triangoli sono
simili hanno gli stessi valori k e k1 pertanto, sostituendo in
kk 1=
9 il valore k = 6 si ottiene che k1=1.5.
.
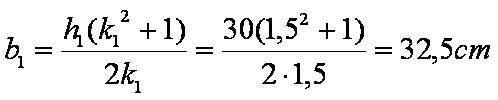Quindi si ha che:
.
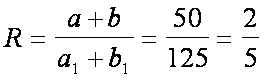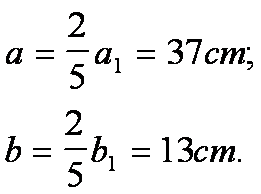
I lati di un
triangolo misurano 13cm, 14cm, 15cm. Quanti rettangoli congruenti tra loro, con
i lati e ed f , contiene
il quadrato costruito sull’altezza relativa al lato maggiore? Quali sono le
loro dimensioni? Quanto misura l’altezza considerata?
Tenendo presenti il teorema
dell’altezza e i rapporti notevoli
di un triangolo, si calcola il valore kk1
che fornisce il numero dei rettangoli richiesti:
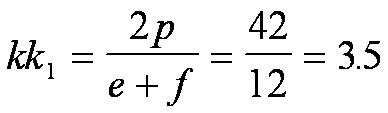
Si calcolano ora le misure e ed
f , cioè:
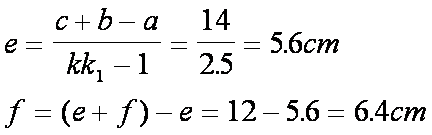
Infine:
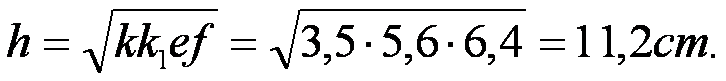
Calcolare
l’area di un triangolo ABC di base AB , sapendo che la somma dei lati AC e BC
misura 50 cm, la loro differenza misura 24 cm e che la base è lunga 40 cm.
Applichiamo la formula:
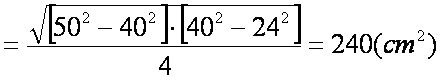
Calcolare le misure
dell’altezza e dei lati di un triangolo, sapendo che:
a+b=150; c=120cm ; k = 6
Si
utilizza il seguente rapporto
notevole:
.
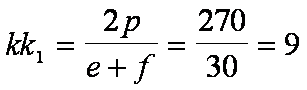Se
kk1 = 9 e k = 6, allora k1 = 1,5.
Da: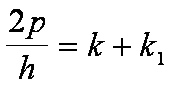 
si
trova che:
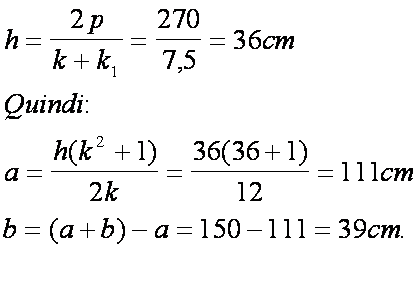
Risolvere un
triangolo ottusangolo ABC, di base AB, sapendo che :
a+c=112cm; b=104cm;
k=13/6.
NOTA.
In questo caso, poiché il triangolo dato è ottusangolo, il piede dell’altezza cade
sul prolungamento del lato AB; pertanto, per definizione, il valore k assegnato si riferisce al rapporto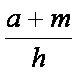 
.
Si utilizzano i dati del problema trovando,
come di consueto, il rapporto tra le
misure note , ossia:
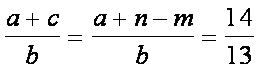(1).
Ponendo
nella (1) :
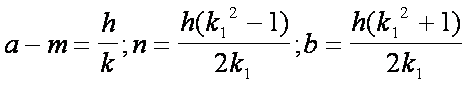
e,
risolvendo l’equazione che si ottiene, cioè: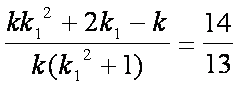 
(ricordiamo che 
), si determina il valore k1=3
, escludendo la radice uguale a 9 che
si riferisce all’angolo acuto minore.
Quindi
si calcolano le misure richieste:
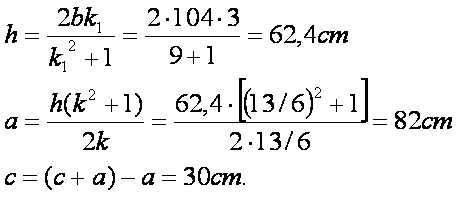
OSSERVAZIONE.
Quando viene data l’ampiezza dell’angolo ottuso di un triangolo, per calcolare il valore k occorre dapprima trovare l’angolo
supplementare di quello dato e, successivamente, applicare la formula 
.
La base di un
triangolo misura 100cm e l’altezza ad essa relativa misura 33cm.
Sapendo che nel quadrato costruito sull’altezza
sono contenuti 11 rettangoli congruenti, ciascuno con le dimensioni e ed
f, calcolare le misure dei lati del
triangolo e le rispettive proiezioni
sulla base.
Per il teorema dell’altezza,
in questo triangolo il valore kk1 è 11.
Poiché è nota la misura dell’altezza,
si calcola quella del raggio inscritto nel triangolo:
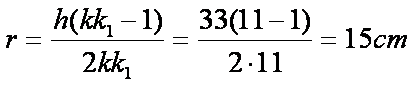
e, successivamente, il valore k+k1 :
.
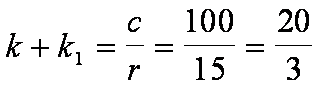Conoscendo k+k1 e kk1
si ha:
11/3
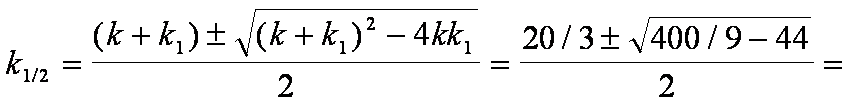
3
Applicando opportunamente le
formule trovate in questo lavoro, si ottengono le misure richieste:
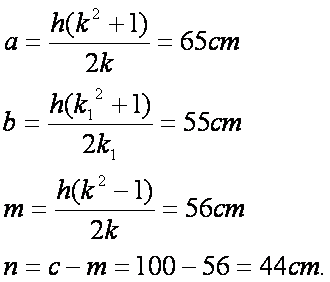
Il perimetro
di un triangolo è 90 cm e nel quadrato costruito sull'altezza di uno dei suoi
lati sono contenuti 9 rettangoli congruenti, ciascuno dei quali ha le
dimensioni e ed f. Si chiede quanto misura il lato su cui cade tale altezza e,
considerato l'insieme dei triangoli isoperimetrici a quello dato, qual è la
misura dell'altezza relativa all'ipotenusa di un triangolo rettangolo.
Dal teorema dell'altezza si
deduce che kk1= 9, pertanto
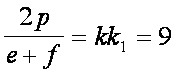
Il lettore è pregato di
trovare le soluzioni richieste. Facile, vero?