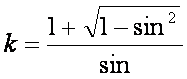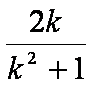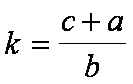Natura trigonometrica di k

Dalla relazione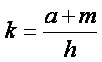 si ricava che:

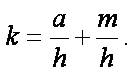     (48)

Ponendo nella (48):

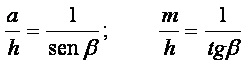  si ha:

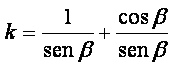
da cui si ottiene:

Fino a quando non sarà costruita una particolare calcolatrice che associ automaticamente al valore dell’angolo b il corrispondente valore k e viceversa (evitando il linguaggio trigonometrico), si userà una normale calcolatrice scientifica.

ESEMPI

Nota la misura dell’angolo b, per calcolare il corrispondente valore k si procede nel seguente modo:

prima si digita la misura dell’angolo e si preme il tasto sin, poi si applica la formula:

Noto il valore k di un triangolo, si può calcolare l’ampiezza del corrispondente angolo b digitando il numero che risulta dal rapporto e premendo i tasti 2nd + sin.

Ad esempio, se k = 3, si digita il numero 0,6 che si ottiene da 2k e si calcola

k² +1

l’ampiezza b premendo 2nd + sin.

Sul dispay appare il valore di b che è 36,8698…… = 36° 52’ 11” 6.

Applicazioni al triangolo rettangolo

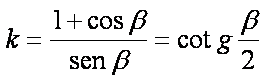
NOTA

Qui di seguito è data una formula empirica che consente di calcolare, con buona approssimazione senza l’uso di una calcolatrice scientifica, l’ampiezza di uno degli angoli acuti di un triangolo rettangolo, noto k.

Attenzione! Per gli angoli di ampiezza 45°, 30° e 60° tali valori sono esatti!

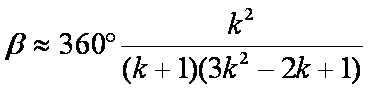(1)

Per esempio,

se k=2 b= 53,33…°

se k=3 b= 36,81…°

E’ facile verificare che la (1) è equivalente alla (2):

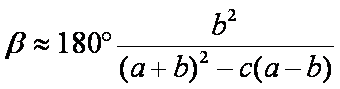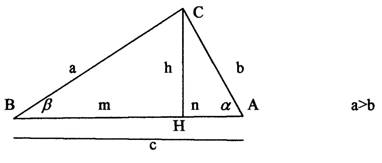
(2) (con a>b; a,b,c, indicano rispettivamente le misure dei cateti e dell’ipotenusa di un triangolo rettangolo ABC, retto in })

TABELLA

Nella seguente tabella sono riportati i valori degli angoli acuti di alcuni triangoli rettangoli, ottenuti rispettivamente con la (1) e con una calcolatrice scientifica.

Si nota subito che i due risultati si avvicinano notevolmente.

E’ auspicabile che si trovi una formula analoga alla (1) mediante la quale si possano ottenere risultati uguali a quelli che ora si hanno con una calcolatrice scientifica. E’ una sfida per il lettore!

Misure lati triangoli rettangoli b a c (in cm)		Valori di Ottenuti con la (1) in gradi decimali	Valori di ottenuti con una calcolatrice scientifica in gradi decimali
3 4 5	3	36,81…	36,86…
5 12 13	5	22,72…	22,61…
7 24 25	7	16,45…	16,26…
8 15 17	4	28,09…	28,07…
9 40 41	9	12,90…	12,68…
11 60 61	11	10,61…	10,38…
12 35 37	6	19,08…	18,92…
13 84 85	13	9,016…	8,79…
20 21 29	2,5	43,58…	43,60…
28 45 53	3,5	31,86…	31,89…
15 112 113	15	7,83…	7,62…
39 80 89	13/3	26,04…	25,98…
48 55 73	8/3	41,06…	41,11…
16 63 65	8	14,46…	14,25…
17 144 145	17	6,93…	6,73…
36 77 85	4,5	25,12…	25,05…
65 72 97	2,6	42,03…	42,07
19 180 181	19	6,21…	6,02…
51 140 149	17/3	20,16…	20,01…
60 91 109	10/3	33,36…	33,39…

SOMMARIO