In ogni triangolo rettangolo, in cui c rappresenta la misura dell’ipotenusa e
a e b le misure dei cateti,
detto k il rapporto 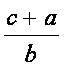 e k1 il rapporto
e k1 il rapporto 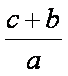 (o viceversa)
sussiste la relazione
(o viceversa)
sussiste la relazione 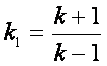 .
.
DIMOSTRAZIONE.
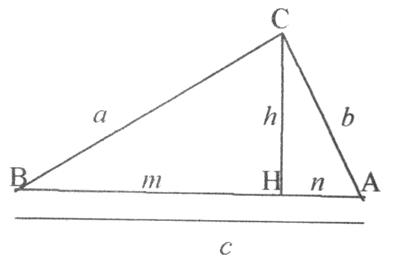
Assegnato un triangolo rettangolo
ABC, retto in Ĉ, si tracci l’altezza relativa all’ipotenusa e siano a, b, c, m, n, h, rispettivamente le
misure dei cateti, dell’ipotenusa, delle proiezioni dei cateti sull’ipotenusa e
dell’altezza ad essa relativa (Fig. 2).
|
|
Fig. 2
Per
la dimostrazione della tesi, si scrive la formula che consente di calcolare la
misura dell’altezza relativa all’ipotenusa di un triangolo rettangolo:
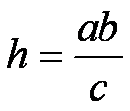 (12)
(12)
e
si pongono in essa al posto di a, b, c,
le formule trovate precedentemente nell’introduzione
(che riporto qui per comodità), ossia:
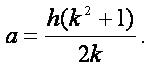
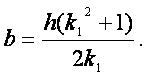
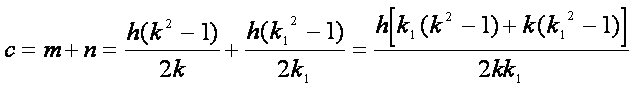 (13)
(13)
Quindi
si ha:
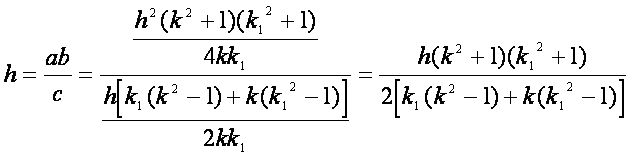 (14)
(14)
Dalla
(14), dividendo per h entrambi i
membri dell’uguaglianza, si ottiene che:
![]() (15)
(15)
Dalla
(15) si trova ![]() in funzione di
in funzione di ![]() :
:
![]() (16)
(16)
ordinando
e cambiando il segno si ha:
![]() (17)
(17)
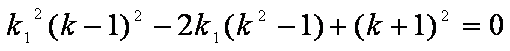 (18)
(18)
e,
risolvendo si giunge alla tesi:
 (19)
(19)
Poiché
![]() le due radici sono
coincidenti.
le due radici sono
coincidenti.
Quindi,
in definitiva, si ottiene che:
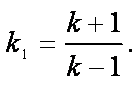 c.v.d.
c.v.d.
NOTAZIONE
Abbiamo posto 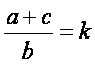 e
e 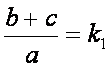
Ma, in uno stesso triangolo rettangolo,
per la similitudine dei triangoli BHC , AHC …, sussistono le seguenti catene di
rapporti uguali:
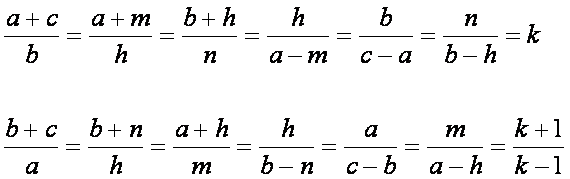
Il lettore può facilmente
verificare che due triangoli rettangoli sono simili tra loro se, e solo se, hanno lo stesso valore k .
COROLLARIO 1. Una delle
conseguenze del teorema ![]() è che, sostituendo
nelle formule date nell’introduzione , a
è che, sostituendo
nelle formule date nell’introduzione , a ![]() il valore
il valore ![]() , si hanno tutti gli
elementi di un triangolo rettangolo in funzione di h e k :
, si hanno tutti gli
elementi di un triangolo rettangolo in funzione di h e k :
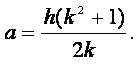 (20)
(20)
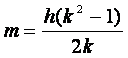 . (21)
. (21)
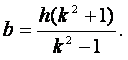 (22)
(22)
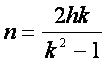 . (23)
. (23)
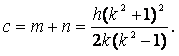 (24)
(24)
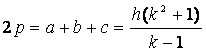 . (25)
. (25)
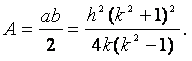 (26)
(26)
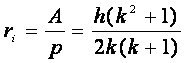 . (27) ri indica la misura del raggio della
circonferenza inscritta nel triangolo.
. (27) ri indica la misura del raggio della
circonferenza inscritta nel triangolo.
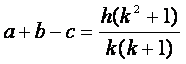 . (28)
. (28)
Mettendo in rapporto a due a due le precedenti formule,
se ne ottengono altre, come ad esempio:
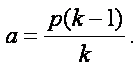 (29)
(29)
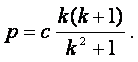 (30)
(30)
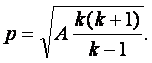 (31)
(31)
Dal confronto della (27) e (28) risulta che in un triangolo
rettangolo 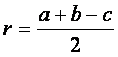 e quindi
e quindi 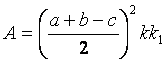 da cui scaturisce che:
da cui scaturisce che:
Ogni triangolo rettangolo è equivalente a tanti
quadrati congruenti tra loro, ciascuno di lato uguale a ![]() , quanti ne indica il prodotto kk1 .
, quanti ne indica il prodotto kk1 .
APPLICAZIONI AI TRIANGOLI
RETTANGOLI