TEOREMI
NUOVI SUI TRIANGOLI
Anna
Montemurro
Introduzione
Come
nasce un nuovo teorema?
Non
è facile rispondere a questa domanda perché questo può avvenire o per caso
oppure mediante un accurato e intenso studio di un determinato argomento o
anche per l’uno e l’altro motivo insieme.
Questo lavoro contiene uno studio sui triangoli, dai quali, appunto,
sono scaturiti i teoremi nuovi presentati nelle pagine seguenti.
Mediante tale studio si giunge alla
risoluzione di un triangolo con un metodo innovativo,
cioè senza ricorrere a difficili
ragionamenti oppure a complicate formule trigonometriche, ma utilizzando
semplicemente il concetto di rapporto tra le misure di due grandezze.
(Such a study shows how to
reach the solution of a triangle using an innovative method which does not
require difficult reasonings or complicated trigonometrical formulas, but
simply uses the concept of ratio between two quantities).
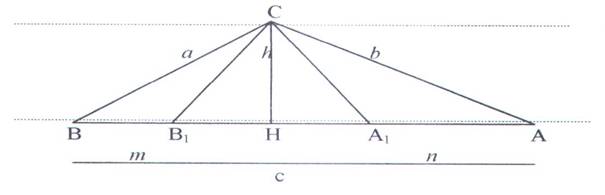
Osservazioni sui triangoli
Si
voglia costruire uno degli infiniti triangoli avente l’altezza assegnata, ad
esempio di 2 cm e calcolare le misure dei suoi lati (Fig. 1).
|
|
Fig.
1
A
tale scopo, si può procedere nel seguente modo:
si
moltiplica la misura h dell’altezza CH prima per un numero
qualsiasi maggiore dell’unità, che ho chiamato fattore k , successivamente per il
suo inverso, ossia per ![]() e si considerano i
prodotti così ottenuti rispettivamente
come la somma del lato a e della sua
proiezione sulla base che è m e come
la loro differenza, per cui risulta:
e si considerano i
prodotti così ottenuti rispettivamente
come la somma del lato a e della sua
proiezione sulla base che è m e come
la loro differenza, per cui risulta:
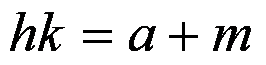 (1)
(1)  (2)
(2)
Tale
procedimento trova conferma nel fatto che, moltiplicando membro a membro la (1)
e la (2), si ottiene la nota relazione:
![]() (3)
(3)
Ora, conoscendo la somma e la
differenza di due segmenti, per trovare la misura di ciascuno di essi, basta
applicare le seguenti formule:
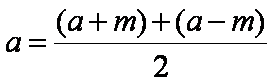 (4)
(4) 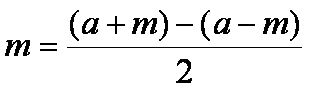 (5)
(5)
Sostituendo nelle (4) e (5) i
valori corrispondenti delle (1) e (2), si ottiene che:
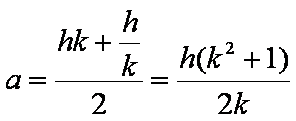 (6)
(6) 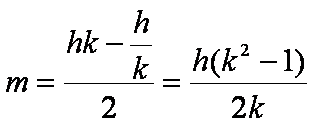 (7)
(7)
Con un procedimento analogo
al precedente, scegliendo un altro numero qualsiasi maggiore dell’unità, che ho
chiamato fattore k1, si
costruiscono ![]() ,
, ![]() e si calcolano le misure b
ed n.
e si calcolano le misure b
ed n.
Quindi
si ha:
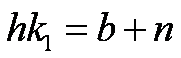 (8)
(8) 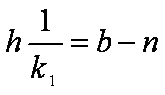 (9)
(9)
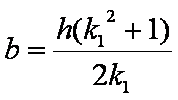 (10)
(10) 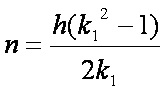 (11)
(11)
Le (6) e (7), (10) e (11) consentono di calcolare
le misure dei lati di uno degli infiniti triangoli aventi altezza 2 cm, da noi
costruito.
Poiché tra gli infiniti
triangoli che hanno altezza 2 cm esistono anche i triangoli rettangoli (nei quali
tale altezza diventa quella relativa all'ipotenusa o un cateto stesso), ci si
chiede:
Di un triangolo rettangolo, è necessario conoscere
entrambi i valori k e k1? Certamente no!
Allora, qual è la relazione che lega k e k1
in un triangolo rettangolo?
Dalle precedenti osservazioni
scaturiscono:
il teorema k (di Montemurro) e
il teorema dell'altezza (di Montemurro).
Applicazioni al triangolo
rettangolo